An invariant approach to statistical analysis of shapes
By S. Lele and JT Richtsmeier
Interdisciplinary studies in statistics series.
2001 Chapman and Hall – CRC press, London.

From the Preface of Lele and Richtsmeier (2001)
Quantitative study of form and form change comprises the field of morphometrics. This field has had a long history. Cuvier (1828) was probably the first biologist to verbalize the dictum “form follows function”. Charles Darwin’s work on theory of natural selection and evolution relied heavily on the study of form and especially variation in form (Darwin, 1859). The seminal work of D’Arcy Thompson (Thompson, 1917) formulated the subject in detail. More recent work in this field has always reverted back to Thompson, either to clarify or to repudiate novel approaches and ideas. Substantial developments in both biological and statistical aspects of morphometrics occurred over the next several decades of the twentieth century. Work by Mahalanobis, Rao and their colleagues initiated the use of multivariate statistical analysis for classification of organisms into groups. Julian Huxley (Huxley, 1932) formulated the field of allometry studying the relationship between size and shape of organisms. James Mosimann (1970) constructed a proper statistical foundation for the ideas of size, shape and allometry. The method of superimposition, particularly the Procrustes superimposition, was developed and introduced to the biological sciences by the famed anthropologist Franz Boaz and his student Eleanor Phelps (Boas, 1905; Phelps, 1932; see Cole, 1996). Later, Sneath (1967) initiated the use of explicit deformation functions for modeling form change. In the last two decades, the idea of studying form change using superimposition and deformation approaches has been seriously considered and further developed by several individuals. While Bookstein considered the deformation approach, Kendall and his colleagues Mardia, Goodall, Small and others concentrated on superimposition techniques. A particular deformation approach, Finite Element Scaling Analysis, was developed by bioengineers (Lew and Lewis, 1977; Lewis et al., 1980) and then applied to additional biological problems by Cheverud and his colleagues (Cheverud et al., 1983, 1991; Richtsmeier and Cheverud, 1986). However, finite element scaling analysis was never fully embraced by biologists. Some of the reluctance felt by biologists stemmed from the seemingly complex mathematics that served as the foundation of the finite element method, but the lack of invariance of this method and other superimposition techniques was recognized (Moyers and Bookstein, 1982; Cheverud and Richtsmeier, 1987; Richtsmeier, 1990). Lele (1991) formalized a precise statement regarding the lack of invariance in morphometrics and provided the solution that is invariant to the arbitrary choice of coordinate system. This monograph summarizes and synthesizes the development of this solution in the context of significant scientific problems. This work is a collaborative effort between a statistician (SL) and a biologist (JTR), each one making the other think more deeply and carefully aboutthe problems and solutions. It is intended for both biologists and statisticians. We have strived to make discussions as mathematically and statistically precise as possible, while keeping “the science”, that is the scientific question posed at the top of our agenda. This book is composed of six chapters. Each chapter has two parts. Chapters 1, 2 and 6 are written to be accessible to all readers. Part 1 of Chapters 3-5 contains notation and mathematical concepts, but is written to be accessible to the quantitative biologist. Part 2 of Chapters 3-5 is targeted towards statisticians, or more advanced quantitative biologists. Included in chapters 2 through 6 are detailed computational algorithms for the implementation of various methods. These are targeted towards statisticians, or more advanced quantitative biologists. The book is organized in this way so that the more difficult mathematical portions can be passed over without loss of continuity, or of understanding.
Book Reviews
Please refer to the attachments for the reviews.
Type | Download | Reviewer |
|---|---|---|
Journal | Biometrics | Ian Dryden
|
Journal | Journal of Human Evolution | Dennis Slice |
Journal | Biometrics Journal | D. Stoyan |
Errata
Partial list of errors in “An invariant approach to statistical analysis of shapes” by Subhash R. Lele and Joan T. Richtsmeier
We apologize to the readers of our book for the many errors. The book was rushed to printing prematurely without our knowledge and many errors were made during production. The book will be reprinted with corrections in the near future, probably in 2002. The corrections are numerous. Some of the more obvious are listed below. We will add more detail as time goes on.
Page numbers given below refer to page numbers in the published book.
General problems
1) The use of “N” versus “n” for sample size. The use is inconsistent and should be “N” throughout the book 2) Preface: This section simply stops mid-sentence. A last word should be added at the end of the last sentence: ” “understanding.” 3) Many of the references are incomplete and incorrect and contain misspellings of authors’ names. This is due to the production staff using a working copy rather than the finished copy. These errors are being updated and corrected. 4) The notation used on page 162 is incorrect: SDM should be SDMB,AM/font> 5) Table 4.5 (page 186) contains a random line (the first line: –1.961) that should be deleted. The whole point of that table is that the confidence interval EXCLUDES the number 0. There are numerous errors in the text on page 186 that discuss this table that are also very misleading. That paragraph should read:“This confidence interval does not contain zero and therefore suggests that the two populations differ significantly in scale. Remember, however, that there is no single value that represents ‘size’ and that this result may change depending upon the chosen scaling factor. Since we found a difference between the samples for this particular measure of ‘size’, differences that have been previously estimated for these samples are considered differences in the shapes of the populations. With evidence for a difference in size, confidence intervals for the estimated shape difference matrix can be examined.”6) Page 189-191. The form difference matrix that begins on page 189 is the same as the form difference matrix presented on page 190, except that the one that begins on page 189 is in vector format and the entries are sorted from minimum value to maximum value. Unfortunately, the first few lines of the vector are given on page 189 and then is interrupted by the form difference matrix on page 190. The last portion of the vector is given on page 191. The vector that starts on page 189 and is continued on page 191 (BUT NOT PAGE 190) is a single vector. The columns on pages 189 and 191 should be labeled: “Linear Distance”, “Estimate”. Page 190 gives the same form difference matrix but written in matrix format and should be presented isolated from the vector. 7) The p-value given at the bottom of page 191 goes with the table that is presented on page 192. 8) Confidence intervals that go from page 192 to 193 span two pages. The column headings on pages 192-193 should read: “Linear distance”, “Lower limit”, “Estimate”, “Higher Limit” 9) Sections 5.7 and 5.8 were switched in order. The published section 5.7 should be numbered 5.8 and should appear AFTER the section that is currently labeled 5.8. In other words Section 5.8 (now on pages 229-230) should be assigned the section number 5.7 and should be put in front of the section entitled, “Statistical analysis of form and shape difference due to growth” on page 226 which should be renumbered as 5.8. 10) There are multiple errors in the figure caption for Figure 5.3 on page 232. It should read:
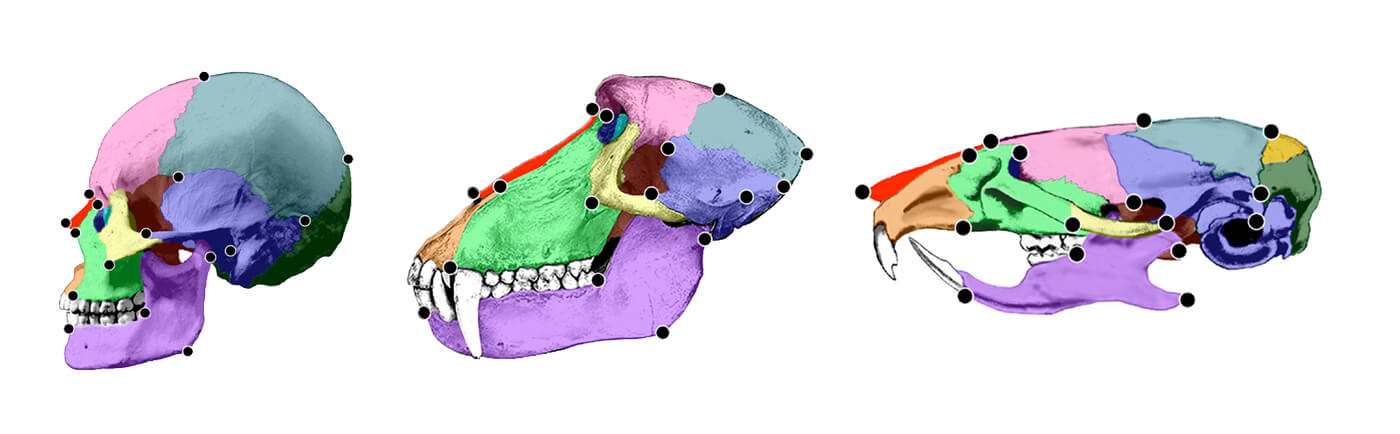
“Figure 5.3 Immature (top left) and adult female (bottom left) skulls of C. apella with location of six facial landmarks used in growth analysis indicated. Immature (top right) and adult female (bottom right) skulls of M. fascicularis are given in the right panel. Landmarks include: 1, nasale; 2, intradentale superior; 3, premaxillary-maxillary junction; 4, zygomaxillare superior; 5, maxillary tuberosity; 6, posterior nasal spine. The posterior nasal spine is located on the sagittal plan and cannot be seen from this view. Its location in this drawing is therefore approximate. Though both immature specimens are from the same developmental age group, the immature M. fascicularis skull is of a younger age than the immature C. apella skull, which accounts for the size difference in these immature specimens. Scale is approximate. Landmark names are given in Table 3.3b.”11) Postlude is full of errors and typos. It should read as follows:
POSTLUDE
This monograph provides the foundations for quantitative analysis of landmark coordinate data based on the invariance principle. In addition to developing the statistical foundations for the study of forms and shapes as represented by landmark coordinate data, we provide descriptions and examples of various applications of our approach. The fields of application in our monograph ranged from Paleontology where the origins of morphometrics lay, to the modern subjects of reconstructive surgery, the phenotypes of genetically engineered animal models, and molecular structure. Where should we go from here? Although we are not visionaries like D’Arcy Thompson, we take this opportunity to speculate about the future of the field and the problems that need to be addressed for the field to progress.
There is tremendous potential for the use of landmark data analysis in the fields of medicine, molecular biology, pattern recognition, computer vision, and biomechanics. One area of study of particular interest to us is the fusion of morphological data and other kinds of data; e.g., behavioral, genetic, life history data. This monograph discussed techniques that are most useful in exploratory or descriptive research. Now is the time to go beyond description and venture into explanation. To accomplish this task, we need to contemplate the construction of models for various processes that might be responsible for form change (e.g., growth, evolution, biomechanical properties, disease, genetic mutations). We hope that the next edition of this monograph will have at least a chapter on explicit, explanatory models for change in the geometry of biological forms. An additional aspect that requires attention is the selection and validation of particular models in experimental and/or natural settings. This includes validation of the Matrix Normal distribution as a sensible perturbation model, and validation of explanatory models proposed by future researchers. Finally, the concept of variability, its role in biological form change, and the use of {\Sigma_{k}}^{\bullet } in the study of biological variability will play a pivotal role in the future applications of our methodology.
We cannot predict the future, but for us it has been an extraordinary journey through the morphometrics landscape. We close with the following quote that we feel particularly appropriate after almost ten years of collaboration.
So easy it seemed once found, which yet unfound most would have thought
impossible.
John Milton12) An early version of section 5.9.1 (that looked at a different data set!) was included in the book by mistake. The updated version follows:
5.9.1 Statistical testing of similarity in growth pattern
Hypothesis testing for similarity in growth pattern
The range of the elements of the growth difference matrix just presented (0.671 – 0.991) indicates that the difference in facial growth in these two species is not simply a matter of scale. Our previous discussion of the differences in growth matrices suggests that there are significant differences in facial growth patterns of these two species. If statistical testing for difference in overall growth pattern is required or desired by the investigator, Gobs can be calculated following methods outlined above and detailed in Chapter 4 for the two-sample case.
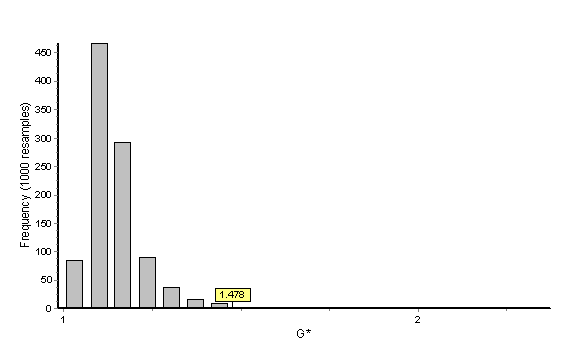
In this example the bootstrap reference sample is Macaca fascicularis (the denominator). The histogram below provides the distribution of 1000 bootstrapped G statistics (each value of a single bootstrapped G statistic is accounted for in the histogram) as well as the placement of Gobs (Gobs = 1.478) within this distribution. The probability is given as 0.006 and Gobs clearly falls outside of the central tendency of the distribution. We reject the null hypothesis that facial growth of Cebus apella is similar to facial growth of Macaca fascicularis. When the test is done using Cebus apella as the reference sample with 1000 bootstraps, the general outcome of the hypothesis test (i.e., rejection of the null hypothesis) is the same but the probability value is 0.0000. The increase in significance level reflects the smaller sample size of the Cebus apella samples and the influence of the sample size in the composition of the bootstrap samples. Remember that these are one-way tests and if sample size permits, the test should be run twice, once using the numerator as the reference sample and again using the denominator as the reference sample.
List of typos and errors in the mathematical parts of the book:
- Page 50, middle of the page: Should read R(\theta), brackets are missing.
- Page 53, line 14: ‘Let M_{i} denote the ..’ . This should read ‘Let M denote the ..’.
- Page 55,line 19: ‘…the following formula’ should read as ‘.. the following formulae’.
- Page 56, line 21: Then A \otimes B … Remove the word ‘Then’.
- Page 62: The quote should be at the beginning of the chapter, not at the beginning of this section.
- Page 77, line 18: ‘…,where V= {\Sigma}_k \times {\Sigma}_d \otimes’ should read as ‘…,where V= {\Sigma}_k \otimes {\Sigma}_d ‘.
- Page 103, lines 20 and 26, page 104, line 9: \varphi_{lm} = \sigma_{ll} + \sigma_{mm} – 2 {\varphi}_{lm} should read as \varphi_{lm} = \sigma_{ll} + \sigma_{mm} – 2{\sigma}_{lm}.
- Page 115, line 6: \varepsilon_{lm}=(\bar{e}_{{lm}}{}^{2}-\frac{3}{2} s^{2}\left(e_{{lm}}\right))^{0.25} should be replaced by \varepsilon_{lm}=(\bar{e}_{{lm}}{}^{2}-\frac{3}{2} s^{2}\left(e_{{lm}}\right))^{0.5}.
- Page 119, line 8: It should read as \sum_{j=1}^{D} \lambda_{j}{ }^{2}\left(\sigma_{11}{ }^{2}+\sigma_{11} \sigma_{11}+\sigma_{11} \delta_{11}{ }^{j}+\sigma_{11} \delta_{11}{ }^{j}+2 \sigma_{11} \delta_{11}{ }^{j}=\operatorname{var}\left(B_{11}\right)\right.
- Page 169, line 25: T_{(-1)} should read T_{(-i)}.
- Page 210, line 16: It should read as FDM(\hat{M}_2,\hat{M}_1)\rightarrow FDM(M_2,M_1)
- Page 227-228: The equation K(K-1)/2 is used many times in the text but the format for the equation varies. Sometimes it is written as just written above (Pg 227) and other times it is written using a large horizontal line to separate numerator and denominator (Pg 228). Why not use a consistent format?
- Page 254: There is a change in the font.
- Page 285, Postlude, line 23: ‘.. at least a chapter on explicit models ..’
- Page 285, postlude, line 24: Should read ‘An additional aspect ..’
- Page 285, postlude, line 27: ‘a sensible perturbation model and validation of explanatory …’
Data Sets
The following datasets are available for download. The trisomic and normal mice datasets come from work supported by the National Science Foundation under Grant No. 0049031: